Athans Blog

Recurrent Neural Networks (RNN)

Vanilla Recurrent Neural Networks (RNN)

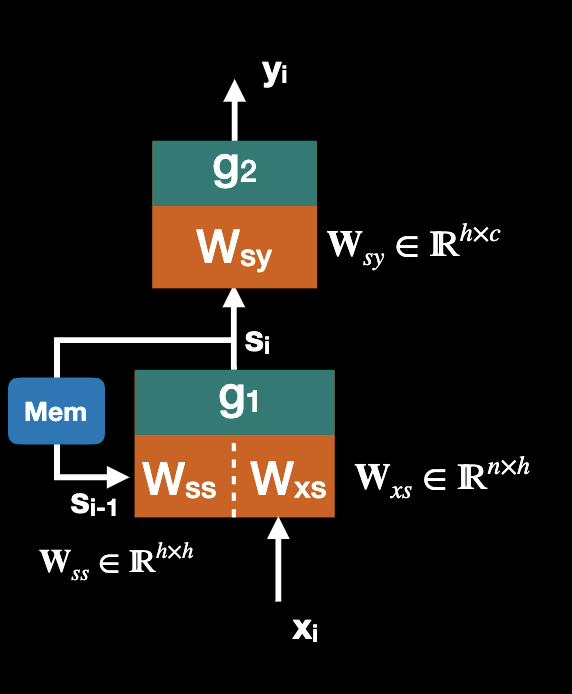
We start with a two layer feed forward network, where input x is a n-D vector representing the sequence elements, output y is C classes, and hidden layer s has h hidden nodes.

Then we have $s=g_1(w_{xs}x+b_s), y=g_2(w_{s_sy}s+b_y)=g_2(w_{s_sy}(g_1(w_{xs}x+b_s))+b_y)$ , where $g_1, g_2$ are activation functions. They are usually tanh and softmax functions respectively.

Now we add in a recurrent loop, this network is called Elman Network. But we noticed x, y, and s are indexed by sequence position i. We brushed under the rug that the state is delayed, and there must be memory to store previous state.

Then we have $s_i=g_1(w_{XS}x_i+w_{ss}s_{i-1}+b_s), y_i=g_2(w_{s_sy}s_{i}+b_y)$, note that $s_0$ state must be initialized, usually with a vector of zeros.

Training and inference

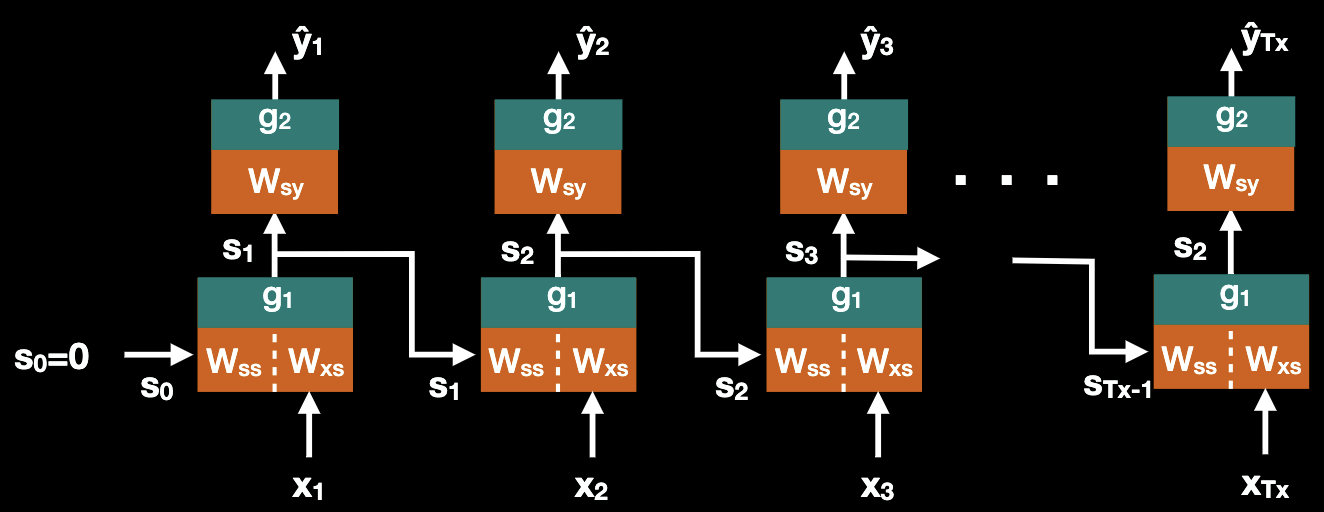
How do we train RNN? We use backdrop with a trick, we initialize state $s_0=0$, with the first input $x_1$ we have $s_1=g_1(w_{XS}x_1+w_{ss}s_0+b_s), y_1=g_2(w_{s_sy}s_1+b_y)$ ; similarly with the second input $x_2$ we have $s_2=g_1(w_{XS}x_2+w_{ss}s_1+b_s), y_2=g_2(w_{s_sy}s_2+b_y)$ ; and with i th input $x_2$ we have $s_i=g_1(w_{XS}x_i+w_{ss}s_{i-1}+b_s), y_i=g_2(w_{s_sy}s_i+b_y)$ . We unroll network over time for sequence of length T, remember all weights $w_{ss}, w_{xs}, w_{sy}$ are shared.

Considering the task of sequence classification, the training pair is

• Input: sequence $x=x_1, x_2,...,x_{T_x}$
• Training label: y is a class represented as a 1-hot vector

We use cross entropy as the loss function. This looks like a feedforward network. We train it using Stochastic Gradient Descent with Adam/RMSprop. The training procedure is called Back Propogation Through Time (BPTT), the unrolled network is deep with number of layers equals $T_x+1$. And if loss function is defined over full output sequence, it’s still trainable by backdrop (BPTT).

This unrolling looks complicated to implement, yet it’s already implemented as part of training in the deep learning frameworks (Tensorflow, PyTorch, etc.)

Statistical Language models

A statistical language model is a probability distribution over sequence of words computed from some corpus. Consider a one word sequence, $P(x_1)$ is just the probability of each word, which can be represented as a histogram. Now consider a two word sequence, $P(x_1, x_2)$ is the probability of ordered word pairs.

• Is $P(x_1, x_2) = P(x_2, x_1)$?

  No, It’s not symmetric as $P('Two', 'Sigma') != P('Sigma', 'Two')$

• Is $P(x_1, x_2) = P(x_1)P(x_2)$?

  No, the two words are not independent either

Keep going bigger, $P(x_1, x_2, x_3, x_4, x_5)$ is the probability of a sequence of five words being used in the language. Examples are P(‘the’, ‘cat’, ‘in’, ‘the’, ‘hat’) is the probability of the “The cat in the hat” appearing in a corpus of English text. P(‘a’, ‘q’, ‘t’, ‘i’, ‘u’) is the probability of the letter sequence “aqtiu” appearing in a corpus of English text. To fully represented English language, we would need a histogram with a exponential number of cells, say $10,000^5$ for 5 word sequence.

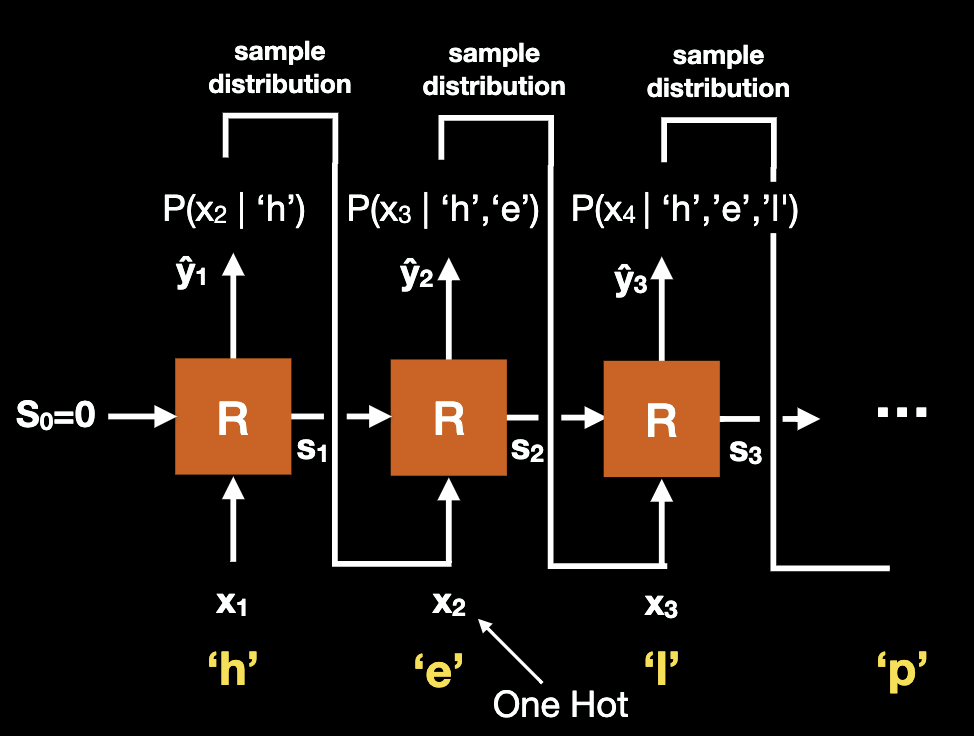
Let’s visit an example of using Character RNN implementing a language model. We assume x is an n-dimensional one-hot encoding of characters and includes punctuation, space (end of word). $\hat y$ is also n-dimensional, but values are not limited to 0/1. In the RNN, final activation function is softmax, each output comprising $\hat y$ can be viewed as the conditional probability of the next character. When a sequence $x_1, x_2,..., x_n$ has been input to a trained network, the output $\hat y_n$ is the probability distribution $P(x_{n+1}|x_1, x_2,..., x_n)$

The network is trained using cross entropy loss to compare the next character from the training set $x_{i+1}$ to the output $\hat y_i$ from the network. The training process takes sequences of characters, and put them in one at a time, comparing the predicted character to the next one.

How do we sample the output $\hat y_i$? Recall $\hat y_i$is a vector of dimension equal to dictionary size, we will follow the steps:

1. Take largest value (arg max)
2. Randomly sample based on distribution.
3. Blend using “temperature” of softmax function.

And how complicated is to code this up?

Teacher Forcing

The question raised from the chart above, what should $x_2$ be? We have several choices:

1. Raw output $\hat y_1$ of RNN
2. A sampling of $\hat y_1$ e.g. 1-Hot with one at arg max $\hat y_1$ position.
3. Teacher forcing: Use the actual $y_1$ rather than a sampling of $\hat y_1$. In this example, $x_2$ is ‘e’.

The advantages of Teacher Forcing is that it makes training more robust since errors don't accumulate, and the training converges faster. The disadvantage is that Inference is different than training which leads to exposure bias. Some alternatives to Teacher Forcing include Curriculum Learning and Professor Forcing.

Vanishing and exploding gradients

The problems with Vanilla RNN are mainly vanishing and exploding gradients:

• Exploding gradients

  Solution: Gradient clipping

• Vanishing gradients

  Solution: Regularization

• Information doesn't propagate far back in time and easier elements of input sequence don't affect output.

  Solution: Tastier network such as LSTM and GRU, these networks are also less prone to vanishing/exploding gradient problems.